


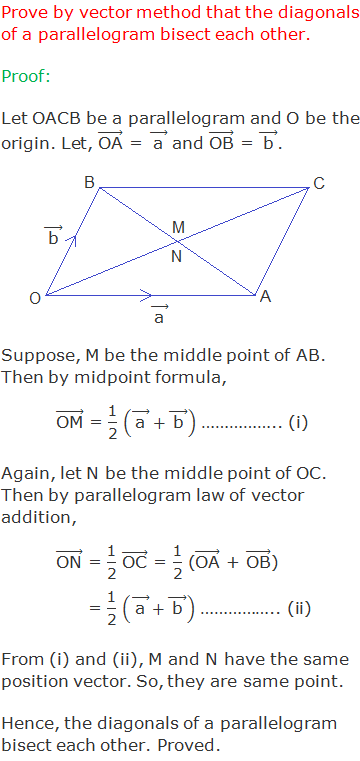
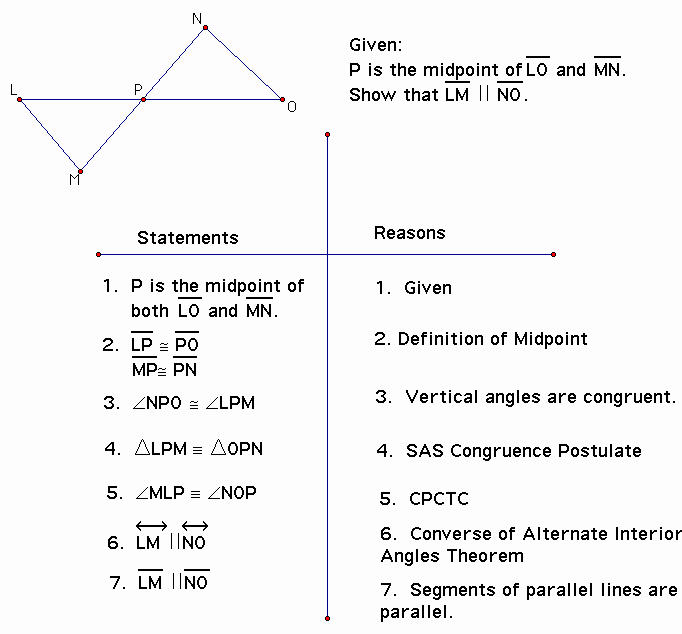
Add that there are a few things that we need to pay attention to when we’re using two-column proofs, such as: Use this video as an illustration of the two-column proof. Point out to students that you will be using two-column proofs in this lesson. Two-column proofs are a good starting point for students in geometry and are most frequently used in geometry classes. Since two-column proofs are highly structured, they’re often very useful for analyzing every step of the process of proving a theorem. Two-column proofs are proofs that contain two columns – in the first column, we place the statements, whereas in the second column we place the reasons, i.e. This is typically a detailed and lengthy paragraph where we explain our reasoning in detail. You can define the paragraph proof as a type of proof where, as the name suggests, we use a paragraph to prove a theorem. The flow-chart proof is praised for its visualization component, as it enables us to easily visualize how the conclusion results from the progression of statements. In this type of proof, we show how the sequence of statements takes place with the help of arrows, i.e. In this proof, we can make subsequent statements from each statement. We write every statement inside a box and provide a reason under this box. Flow-Chart ProofĮxplain that flowchart proofs are proofs in which we use boxes and arrows to organize the statements. Point out that all three ways rely on statements, or the claims that we’re making while proving a theorem, and reasons or the justifications we provide for the statements.
Proofs in geometry calculator how to#
How to Teach Proving Theorems Ways of Proving a ProofĮxplain to students that there are two types of proof: direct proof, where we’re assuming that the statement to be proved is true, and indirect proof, where we’re assuming that the statement to be proved is untrue.Įxplain to students that there are three ways of proving a proof: In a proof, our aim is to use known facts so as to demonstrate that the new statement is also true. A proof is a set of logical arguments that we use when we’re trying to determine the truth of a given theorem. Proving a theorem is just a formal way of justifying your reasoning and answer. Point out that by explaining how we reached our answers, we’re showing our reasoning to others so that we convince them of the validity of each step and get them to agree with us, ideally. To explain what we mean by proving theorems, you can start by reminding them of expressions like these. Unlike a postulate, a theorem is a statement that we can demonstrate and prove to be true.īut what does it mean to “prove” something? By now, students have already been asked in different grades to “justify” or “explain their answer”. Thus, we use postulates and previously proven theorems to prove theorems. Postulates are used to explain undefined terms, and also, to assist us in proving other statements. An example of a postulate is this statement: “a line contains at least two points”. When we talk about a postulate in geometry, we’re referring to a statement that is assumed to be true without proof.
So if you’re a math teacher looking for guidance on how to teach this challenging topic, look no further! In this article, we’ve compiled awesome guidelines on teaching how to prove theorems in geometry! Read on to learn more. Much of their work in geometry will consist of proving theorems.Īnd even for the best of math students, this can be a bit of a challenge! This is because proving theorems essentially relies on logical arguments and deductive reasoning, in addition to a solid knowledge of previous math axioms. For example, they’ve come across the Pythagorean Theorem in earlier grades.
When students start learning about proving theorems, they already have some knowledge of what a theorem is.


 0 kommentar(er)
0 kommentar(er)
